COMET method - a new quality in decision making

Currently existing multi-criteria decision-making (MCDM) methods yield results that may be questionable and unreliable. These methods very often ignore the issue of rank reversal paradox, which is a fundamental and essential challenge of MCDM methods. In response to this challenge, the Characteristic Objects Method (COMET) was developed. The classical COMET is entirely free of the rank reversal paradox.

COMET section - fundamental information about COMET algorithm
COMET software - COMET software with manual
References section - the most important papers about COMET
Contact section - contact to the author

COMET

This webpage presents preliminaries of the fuzzy sets theory and computational algorithm of the basic COMET method. In the Software section, COMET software and manual can be founded.

Fuzzy sets theory: preliminaries

Definition 1 The fuzzy set and the membership function
The characteristic function μA of a crisp set A ⊆ X assigns a value of either 0 or 1 to each member of X, as well as the crisp sets only allow a full membership μA(x)=1 or no membership at all μA(x)=0. This function can be generalized to a function μà so that the value assigned to the element of the universal set X falls within a specified range, i.e., μà : X → [0, 1]. The assigned value indicates the degree of membership of the element in the set à . The function μà is called a membership function and the set à ={(x,μà (x))}, where x ∈ X, defined by μà (x) for each x ∈ X, is called a fuzzy set.

Definition 2 The triangular fuzzy number (TFN)
A fuzzy set Ã, defined on the universal set of real numbers R, is told to be a triangular fuzzy number Ã(a,m,b) if its membership function has the following form:
equation1
and the following characteristics:
x1, x2 ∈ [a, b] ∧ x2 > x1 ⇒ μÃ(x2) > μÃ(x1)
x1, x2 ∈ [b, c] ∧ x2 > x1 ⇒ μÃ(x2) < μÃ(x1)

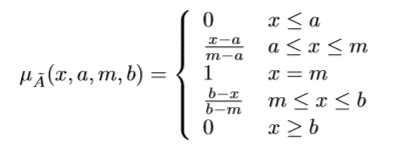
An example of triangular fuzzy number Ã(a,m,b) is presented:
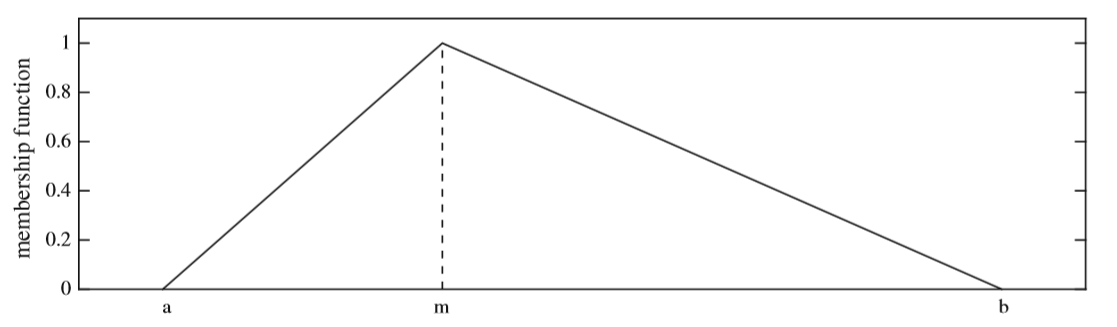
tfnExample
Definition 3 The support of a TFN Ã
The support of a TFN à is defined as a crisp subset of the à set in which all elements have a non-zero membership value in the à set:
S(Ã) = {x: μ{Ã}(x) > 0} = [a, b]
Definition 4 The core of a TFN Ã
The core of a TFN Ã is a singleton (one-element fuzzy set) with the membership value equal to 1:
C(Ã) = {x: μÃ(x) = 1} = m
Definition 5 The fuzzy rule
The single fuzzy rule can be based on the Modus Ponens tautology. The reasoning process uses the IF-THEN, OR and AND logical connectives.

Definition 6 The rule base
The rule base consists of logical rules determining the causal relationships existing in the system between the input and output fuzzy sets.

Definition 7 The T-norm operator: product
The T-norm operator is a T function modeling the AND intersection operation of two or more fuzzy numbers, e.g. Ã and &Btilde;$. In the basic approach, only the ordinary product of real numbers is used as the T-norm operator:
μA(x) AND μB(y) = μA(x) · μB(y)

The Characteristic Objects Method

Step 1. Definition of the space of the problem
The expert determines the dimensionality of the problem by selecting r criteria, C1, C2, ..., Cr. Then, a set of fuzzy numbers is selected for each criterion Ci, e.g. {Ci1, Ci2, ..., Cici}:
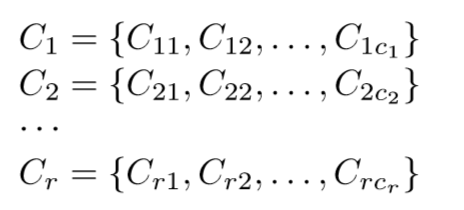
equation2
where c1,c2, ...,cr are the ordinals of the fuzzy numbers for all criteria.

Step 2. Generation of the characteristic objects
The characteristic objects CO are obtained with the usage of the Cartesian product of the fuzzy numbers' cores of all the criteria:
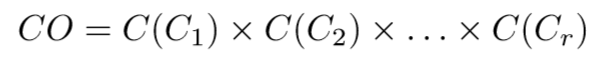
equation3
As a result, an ordered set of all $CO$ is obtained:
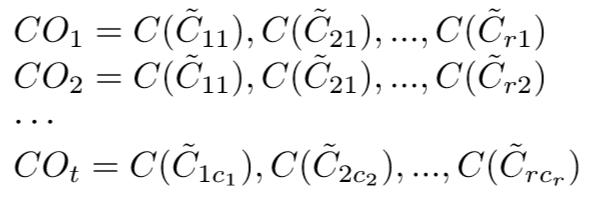
equation4
where t is the count of COs and is equal to:
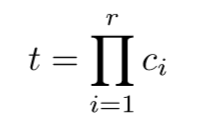
equation5


Step 3. Evaluation of the characteristic objects
The expert determines the Matrix of Expert Judgment )MEJ) by comparing the COs pairwise. The matrix is presented below:
equation6
where αij is the result of comparing COi and COj by the expert. The function fexp denotes the mental judgment function of the expert. It depends solely on the knowledge of the expert. The expert's preferences can be presented as:
equation7
After the MEJ matrix is prepared, a vertical vector of the Summed Judgments SJ is obtained as follows:
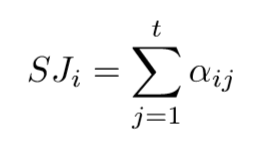
equation8
Eventually, the values of preference are approximated for each characteristic object. As a result, a vertical vector P is obtained, where the i-th row contains the approximate value of preference for COi.

Step 4. The rule base
Each characteristic object and its value of preference is converted to a fuzzy rule as follows:
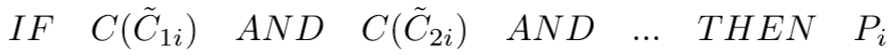
equation9
In this way, a complete fuzzy rule base is obtained.

Step 5. Inference and the final ranking
Each alternative is presented as a set of crisp numbers, e.g.:
Ai={a1i, a2i, ..., ari}
This set corresponds to the criteria C1, C2, ..., Cr. Mamdani's fuzzy inference method is used to compute the preference of the i-th alternative. The rule base guarantees that the obtained results are unequivocal. The COMET is completely free of rank reversal.

Software

Projects

NCN OPUS

A new method for determining the significance level of decision criteria based on characteristic objects

The project aims to develop a new method for determining the significance levels (weights) of decision criteria using characteristic objects. Unlike traditional approaches, the proposed solution considers both global and local weights, accounting for how each criterion's importance changes depending on context and the current “saturation” level of the attribute in question. This makes the evaluation of alternatives in multi-criteria decision-making processes—such as official tenders or product rankings—more accurate and better suited to real-world needs.

The project is supported by the National Science Centre, the agreement no. UMO-2021/41/B/HS4/01296

List of publications:

NCN Preludium

A new method using reference objects to support decision-making process in multi-criteria problems under uncertainty

The objective of the proposed research is to develop a new method using reference objects to support decision-making in multi-criteria problems under uncertainty. The motivation for the proposed research is the fact that in many areas of science, including, behavioral economics, sustainable development or the management, we are dealing more and more with multi-criteria problems whose solution is sought in the conditions of uncertainty. It means that important decision problems involving mostly a lot of contradictory criteria are also considered using imprecise or uncertain data and information.

The project is supported by the National Science Centre, the agreement no. UMO-2016/23/N/HS4/0193

List of publications:

References

Journals

Chapters

Contact

  • Address

    Department of Artificial Intelligence method and Applied Mathematics
    Faculty of Computer Science and Information Technology
    West Pomeranian University of Technology, Szczecin
    ul. Żołnierska 49, 71-210 Szczecin, Poland

  • Email

    wsalabun@wi.zut.edu.pl